线性代数：矩阵变换

二维矩阵变换

缩放变换（Scaling）

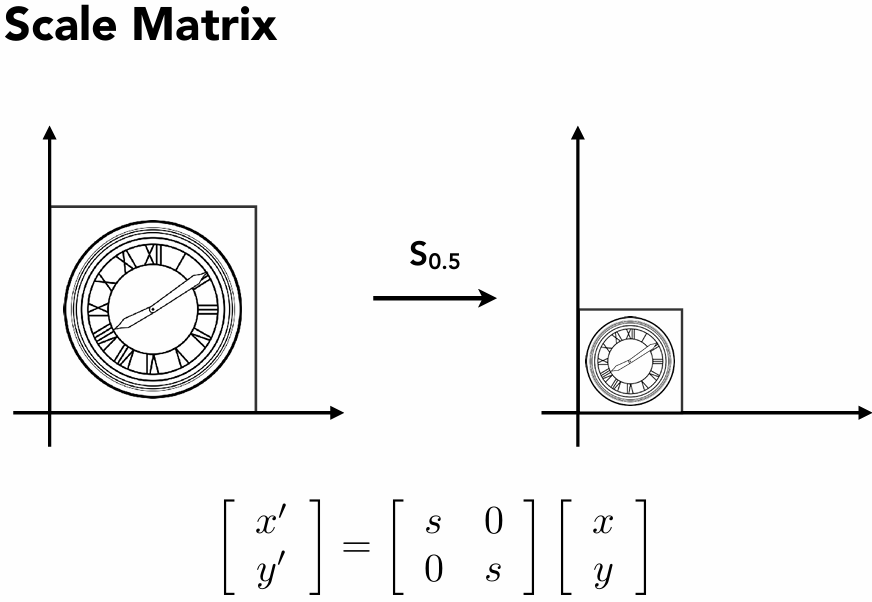
均匀缩放

将矩阵进行缩放，例如将一个矩阵大小均匀缩放变成原来的一半
那么，我们记这个过程为 $S_{0.5}$ 可以写作：

$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s ,0\\ 0 ,s \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$

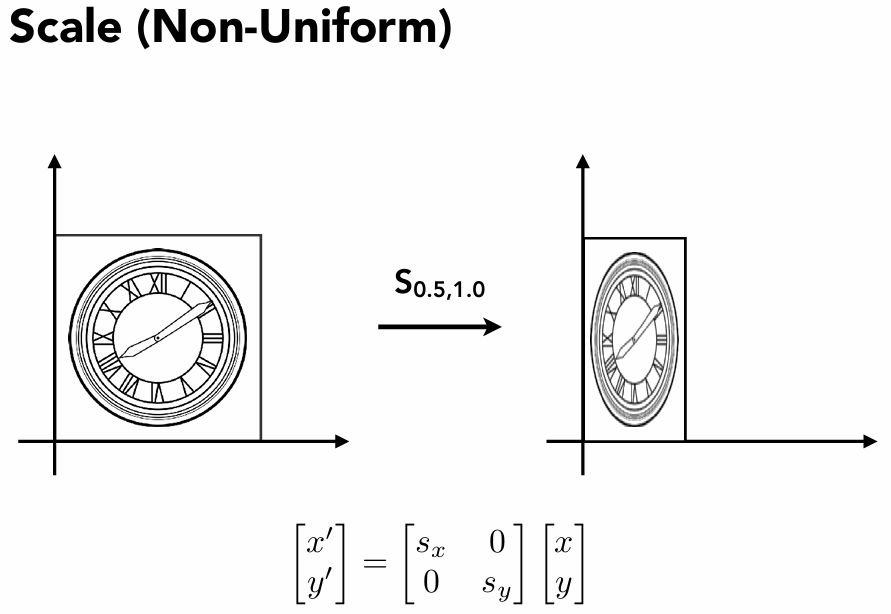
不均匀缩放

现在缩放不均匀，比如x缩放0.5.y不缩放，也就是y不变，x变为0.5非均匀缩放
其实也一样，我们记这个过程为 $S_{0.5，1.0}$ 可以写作：

$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s_x ,0\\ 0 , s_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$

很简单，没什么好说的

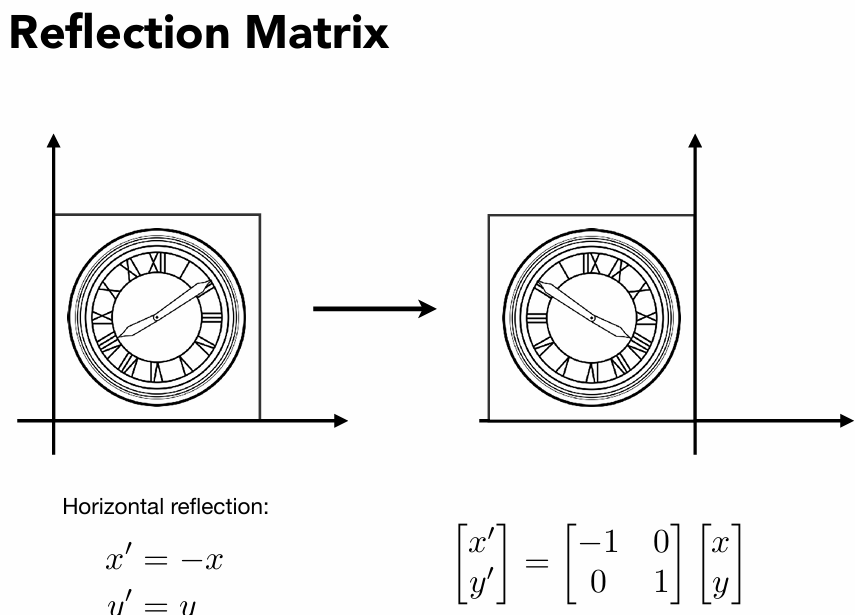
反射变换（Reflection）

关于某条直线的镜像。

1. 关于 x 轴反射：$\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$
   关于 y=x 反射：$\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$
   变换也可也写作：

$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} -1(0) ,0(1)\\ 0(-1) , 1(0) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$

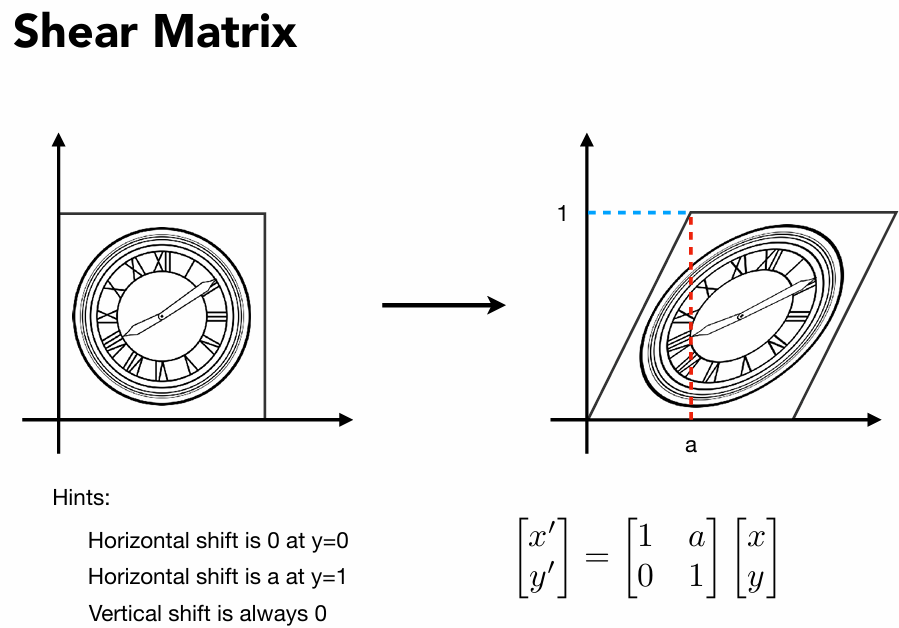
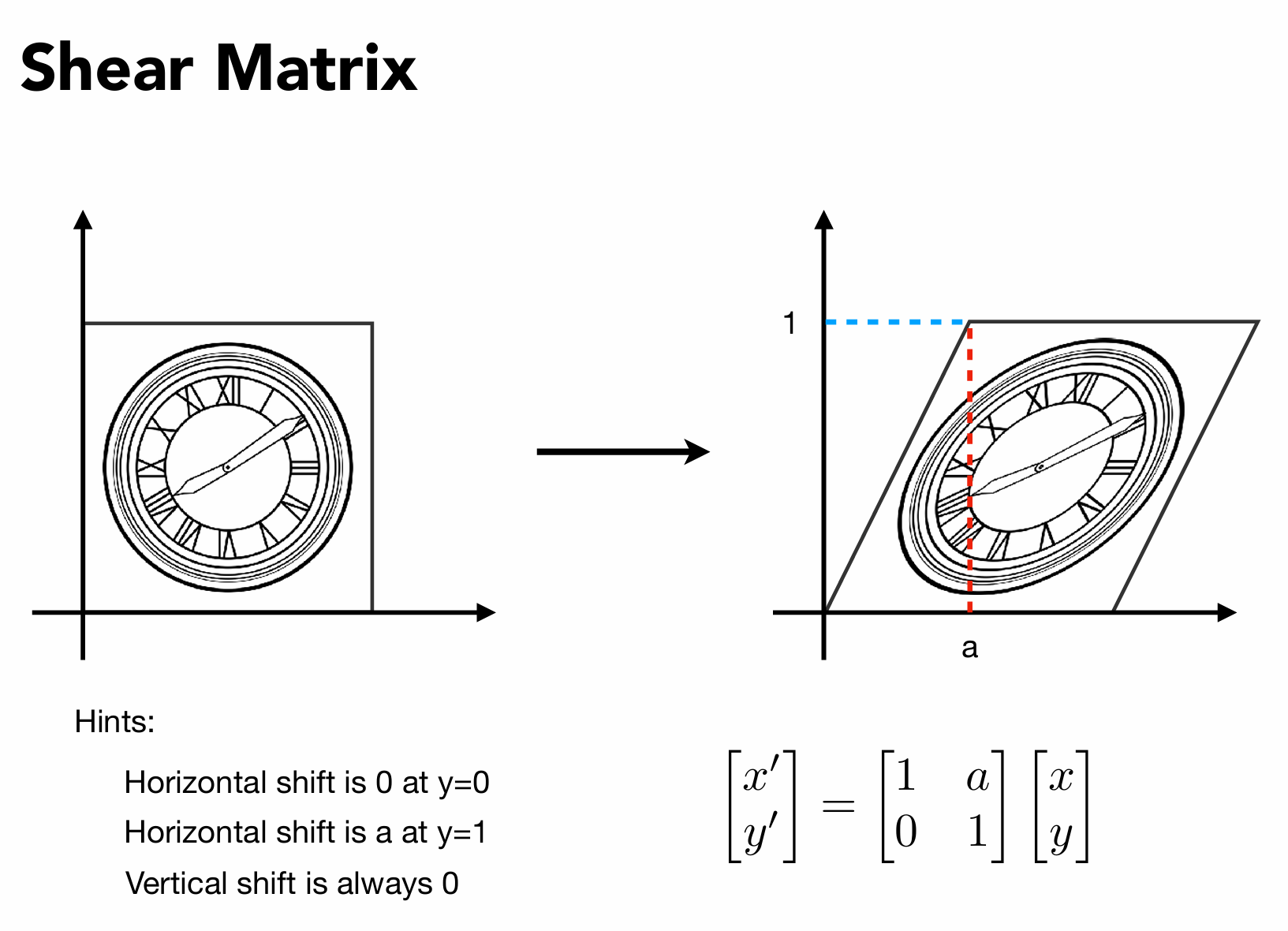
剪切变换（Shear）

简而言之就是沿某方向拉伸。
按照下图所示，上边的每个点向右移动a个单位，竖直(y)不动,下边不动，那就是水平方向的一个切变

$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 ,a\\ 0 , 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$

要找关系，找变化前x，y和变化后x’，y’两者之间关系

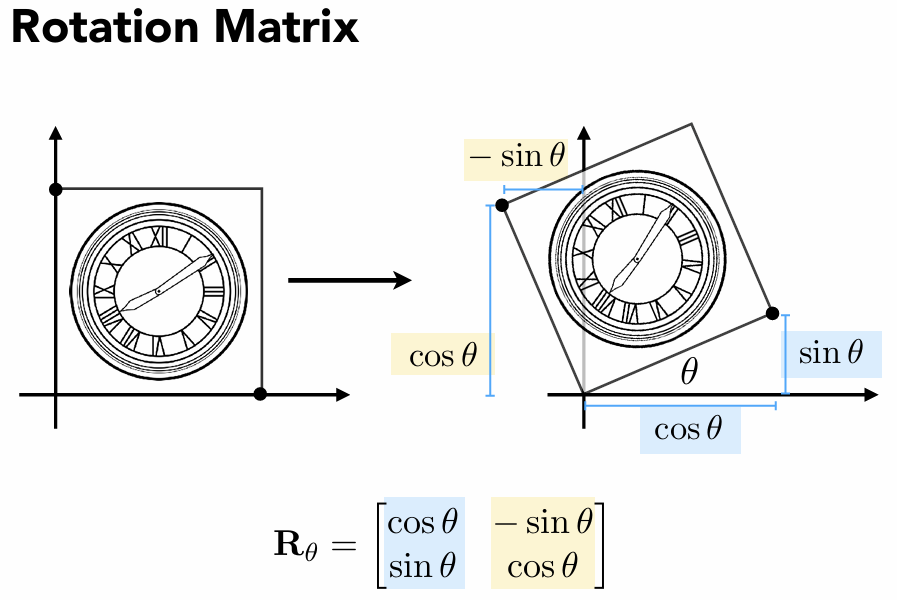
旋转变换（Rotation）

默认规定：

1. 不说明下，说旋转默认绕原点旋转
2. 不说明下，说旋转默认绕逆时针旋转
   例如：将矩阵旋转 $\theta$，则矩阵绕原点逆时针旋转 $\theta$，这个过程可以记作

$R_{\theta} = \begin{bmatrix} cos\theta ,-sin\theta\\ sin\theta , cos\theta \end{bmatrix}$

$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} cos\theta ,-sin\theta\\ sin\theta , cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$

齐次坐标与平移变换

平移变换（Translation）

引入齐次坐标（Homogeneous Coordinates），将平移表示为线性运算
例如：假设将矩阵沿x轴平移 $t_x$ ,沿y轴平移 $t_y$
如果不使用齐次坐标，采用上面的二维形式，只能写成

$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a , b\\ c , d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix} (若单纯平移，则矩阵abcd为单位矩阵)$

不能表示为线性变换，为了统一简单的方法，避免平移变换当作特殊去处理
这时候需要进行降维打击！（bushi），给二维坐标新添加一个维度！
将二维点（Point）表示为 $(x,y,1)^T$ 二维向量（Vector）表示为 $(x,y,0)^T$
就可以看到如下图：

就可以将平移表示为线性运算
以下是为什么定义点为1向量为0：

最底下公式可以得知，点+点之后的结果由齐次坐标表示的是点与点间的中点
很好理解，两个点相加得到的w=2,转换成2D点除掉w后就是对应坐标相加/2了，就是中点
齐次坐标表示变换：

$\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} a , b , t_X \\ c , d , t_y \\ 0 , 0 , 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$

观察会发现矩阵最后一行都是001，平移写在最后一列的前两行上。其余二维线性变换写在左上角的2*2上

用齐次坐标表示线性变换

最后可以得出以下

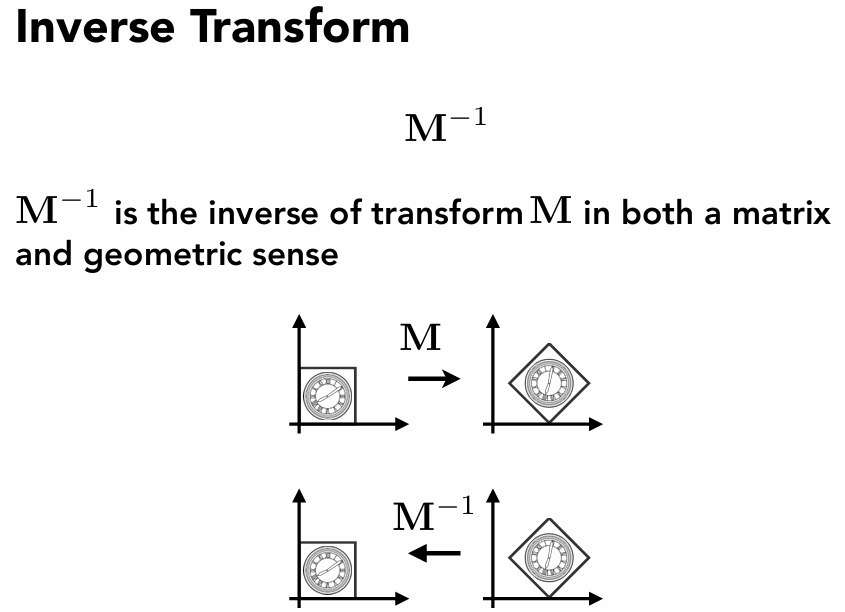
逆变换

很简单，就是变回去（

复合变换

复合变换的初步细节

多个变换可通过矩阵乘法组合，但顺序不可交换。例如，先旋转后平移 ≠ 先平移后旋转。
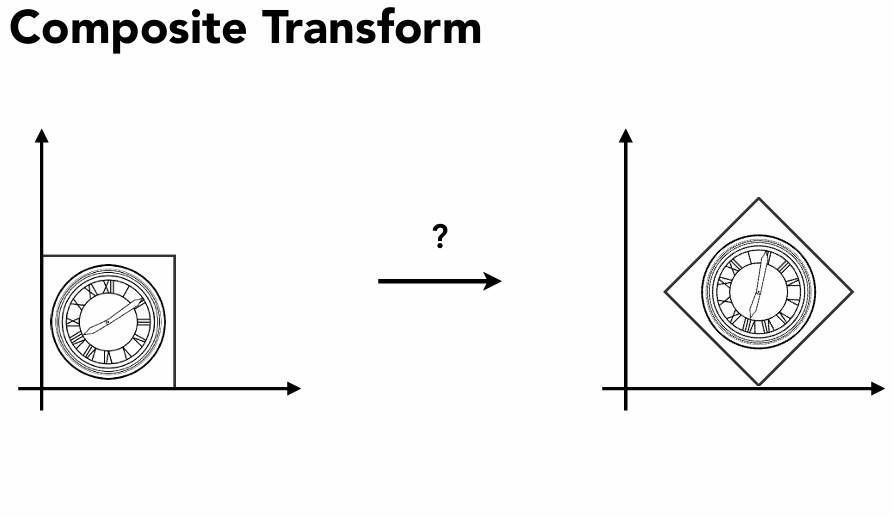
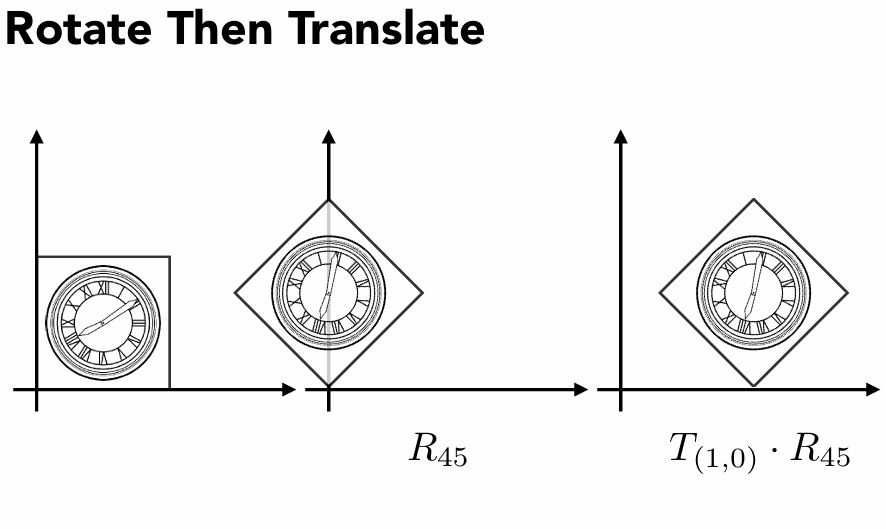
例如以下变换：

思考：如何从左变换到右侧状态
是先平移再旋转？还是先旋转再平移？
先思考，思考完毕之后再看答案
答案：
先旋转再平移
我们上面说了:
1. 先旋转后平移 ≠ 先平移后旋转
2. 不说明下，说旋转默认绕原点旋转
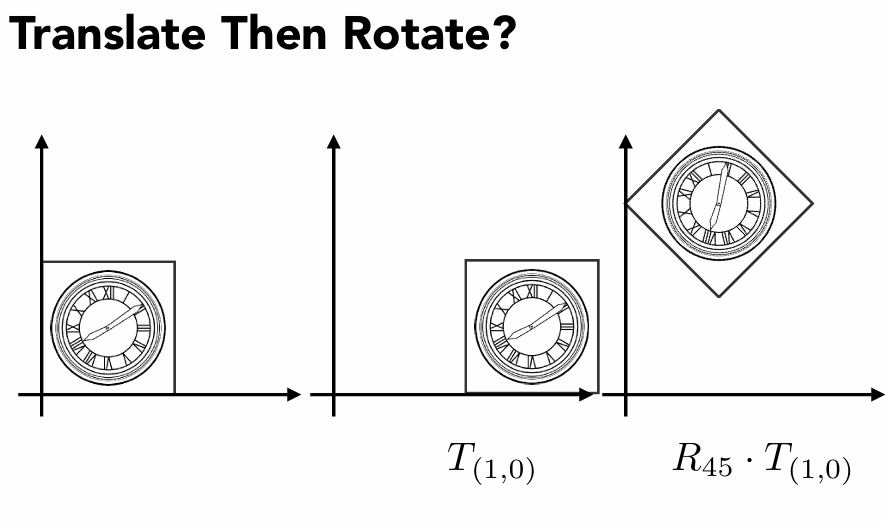
所以会有两种情况：

1. 先平移再旋转 $R_{45} · T_{(1,0)}$

2. 先旋转再平移 $T_{(1,0)} · R_{45}$

矩阵复合变换的小公式

先旋转再平移：

$T_{(1,0)} · R_{45} · \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} 1 , 0 , 1 \\ 0 , 1 , 0 \\ 0 , 0 , 1 \end{bmatrix} \begin{bmatrix} cos\theta , -sin\theta , 0 \\ sin\theta , cos\theta , 0 \\ 0 , 0 , 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

在式子左侧，会发现越先操作的变换越靠近 $\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$ ，从右到左去一个一个应用变换

推广

我们可以先把前面的变换都乘到一块吗，都变成一个矩阵再去乘我们原始的向量

变换分解

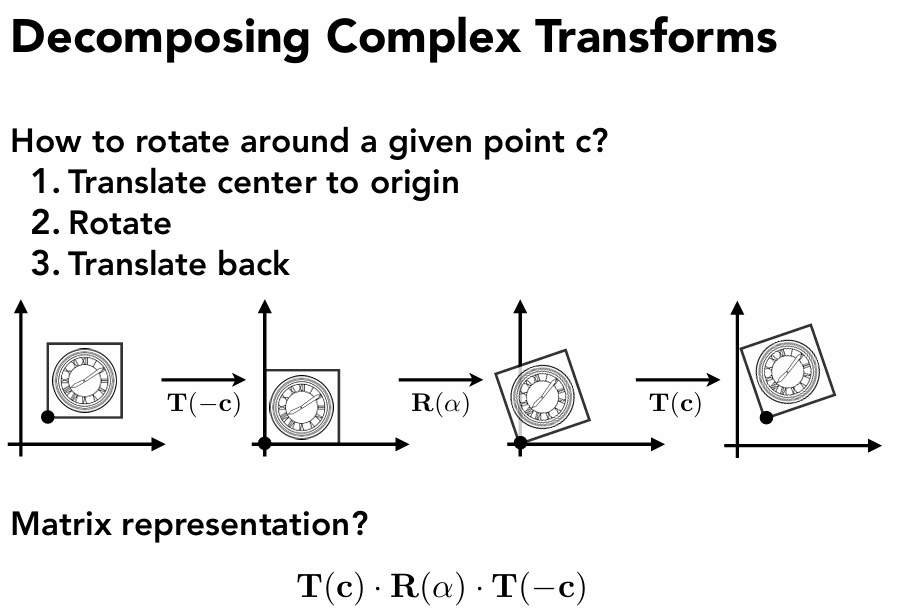
先看图：

我们要实现矩阵绕着点C进行旋转，而非受限与原点旋转。
很简单，先把矩阵平移会到原点上去，再旋转，再平移回去，这样就把绕C旋转这个变换分解成了三个基础变换
$T(c) · R(a) · T(-c)$

浅谈三维变换

基础部分

三维也有基础变换！
为了保证线性运算，使用齐次坐标，依旧要降维打击
三维点齐次坐标 ：$(x,y,z,1)^T$ ; 三维向量齐次坐标 ：$(x,y,z,0)^T$
同二维一样

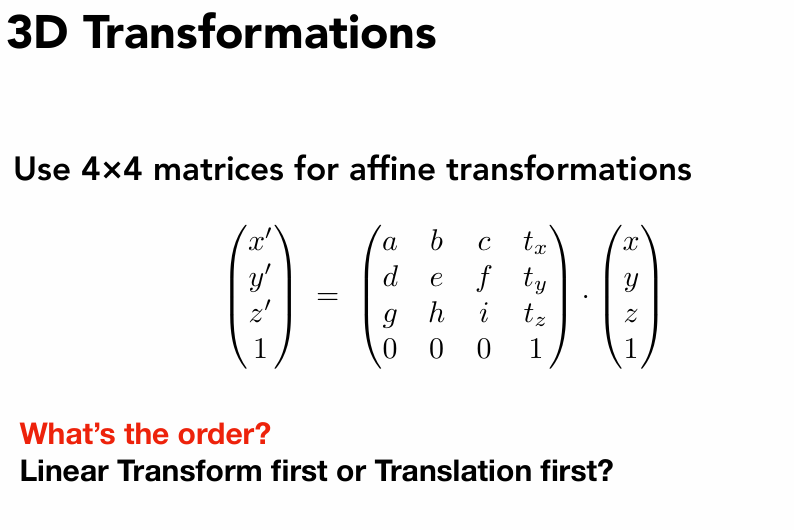
齐次坐标表示变换

一样的啦！

左上角3*3的区域就是三维变换的基础线性变换，右侧最后一列的 $t_x , t_y , t_z$ 表示的是平移，最后一列还是0001

$\begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} a , b , c , t_x \\ d , e , f , t_y \\ g , h , i , t_z \\ 0 , 0 , 0 , 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}$

ArisuMika

关注Arisu喵！关注Arisu谢谢喵！

ArisuMikaのB站

https://space.bilibili.com/355273977