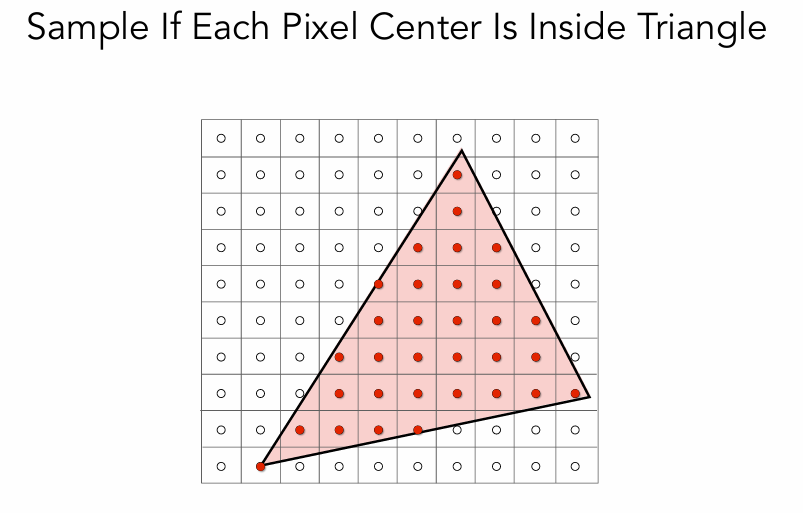
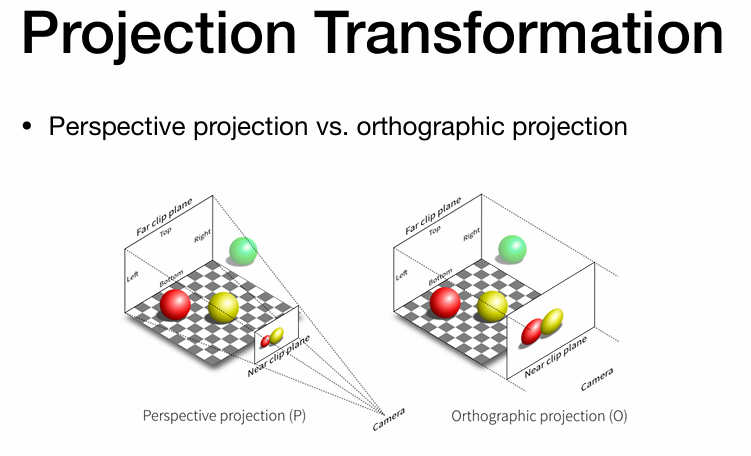
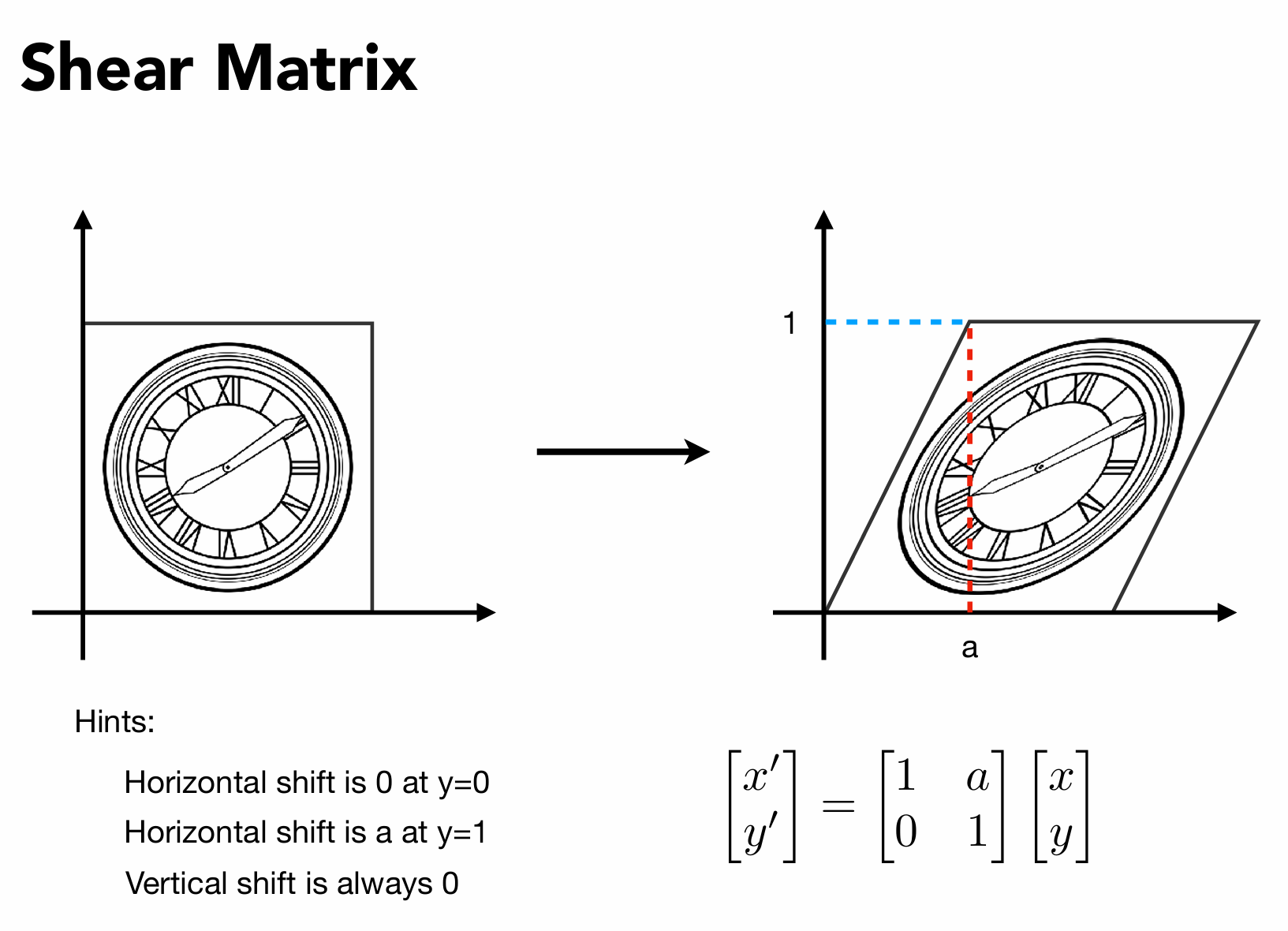
光栅化(三角形的离散化)
在之前的视图变换之后就要进行光栅化 视锥 视锥定义 从摄像机出发,看到的第一个平面是近平面,那么我们要给近平面定义一个宽高度,就类似于显示器一样的宽高比。 也就是可以看到的角度范围:fov,一般分为fovY和fovX。 foxY就是垂直可视角度;fovX也就是水平可视角度。 一般定义宽高比和fovY,直接就可以推出fovX。 具体可以看下图: 视锥计算 确定fovY之后,就可以知道上面角度就是fovY/2,假定近平面上中点坐标是(0,t,n). 就可以列出等式:fovY2=t∣n∣\frac{fovY}{2} = \frac{t}{|n|}2fovY=∣n∣t 宽高比:aspect = rt\frac{r}{t}tr 这些概念都可以相互转换 光栅化(三角形的离散化) 做完MVP(模型、视图、投影变换) 参考本篇文章:变换(模型、视图、投影) 做完上述变换之后,所有的物体都会停留在 [−1,1]3[-1,1]^3[−1,1]3...
变换(模型、视图、投影)
补充知识 众所周知(): Rθ=[cosθ,−sinθsinθ,cosθ]R_{\theta} = \begin{bmatrix} cos\theta , -sin\theta \\ sin\theta , cos\theta \end{bmatrix}Rθ=[cosθ,−sinθsinθ,cosθ] 那问题来了,那我问你,那我问你!如果我要反着转呢?顺时针旋转 θ\thetaθ 角,怎么表示? 嗯?回答我!! 那是不是可以表示为 R−θ=[cosθ,sinθ−sinθ,cosθ]R_{-\theta} = \begin{bmatrix} cos\theta , sin\theta \\ -sin\theta , cos\theta \end{bmatrix}R−θ=[cosθ,sinθ−sinθ,cosθ] 嗯?你回答我,是不是可以把 −θ-\theta−θ 进去! 那是不是也可以看出来:R−θ=[cosθ,sinθ−sinθ,cosθ]=RθTR_{-\theta} = \begin{bmatrix} cos\theta , sin\theta \\...
线性代数:矩阵变换
二维矩阵变换 缩放变换(Scaling) 均匀缩放 将矩阵进行缩放,例如将一个矩阵大小均匀缩放变成原来的一半 那么,我们记这个过程为 S0.5S_{0.5}S0.5 可以写作: [x′y′]=[s,00,s][xy]\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s ,0\\ 0 ,s \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[s,00,s][xy] 不均匀缩放 现在缩放不均匀,比如x缩放0.5.y不缩放,也就是y不变,x变为0.5非均匀缩放 其实也一样,我们记这个过程为 S0.5,1.0S_{0.5,1.0}S0.5,1.0 可以写作: [x′y′]=[sx,00,sy][xy]\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s_x ,0\\ 0 , s_y \end{bmatrix}...
线性代数:向量与基础矩阵
向量 向量加法 不多说,直接加就是了 平行四边形法则或者三角形法则 向量点乘 也没什么好说的,高中数学 有什么用 可以通过向量点乘来判断向量间的夹角,两向量的方向关系 向量叉乘* 叉乘和点乘是完全不一样的计算,向量叉乘仅在三维空间中有定义。对于两个向量a = (a1,a2,a3a_1, a_2, a_3a1,a2,a3)和b=(b1,b2,b3b_1, b_2, b_3b1,b2,b3),它们的叉乘 a×b\mathbf{a} \times \mathbf{b}a×b 的结果垂直于 a\mathbf{a}a 和 b\mathbf{b}b。 1.几何意义 垂直性:叉乘的结果向量垂直于原向量,并且其方向由右手(螺旋)法则(四指从前乘绕向后乘,大拇指方向即为所得叉乘向量方向)决定。 模长:叉乘的模长等于两个向量所构成的平行四边形的面积,即: ∣a×b∣=∣a∣∣b∣sinθ|\mathbf{a} \times \mathbf{b}| = |\mathbf{a}||\mathbf{b}| \sin\theta∣a×b∣=∣a∣∣b∣sinθ 其中 θ\thetaθ...
Windows下VScode配置Eigen
Eigen是一个高层次的C ++库,有效支持线性代数,矩阵和矢量运算,数值分析及其相关的算法。Eigen是一个开源库,从3.1.1版本开始遵从MPL2许可。 缘由 最近在学计算机图形,所以要用到线性代数相关的算法,就自己装了个Eigen,其实用Linux装会简单一些,但是本人懒得搞虚拟机或者双系统了,索性直接在windows装,搞了有些时间,避免后来者碰壁,就自己写一篇教程吧 开始 如果之前没有在Vscode配置过C/C++,请先自行配置 在官网下载Eigen3.4.0 解压到你自己想放的地方,我个人推荐和Mingw32放在一起(别放到子类文件夹去了) 打开VScode在c_cpp_properties.json中设置包含头文件的路径 在”includePath”中加入Eigen的文件路径(注意上一行加逗号) 注意斜杠,要跟图片内一致,不是反斜杠哦 在tasks.json中,修改如下: 同样需要注意上一行后面加逗号。 12"-I","C:\\...\\eigen-3.4.0\\Eigen"...
个人Blog正式上线
个人Blog基本99%完成上线! 本Blog主要展示个人技术栈和日常有趣的事情以及部分教学内容 目前功能 文章发布 音乐播放器 自定义css 最新文档显示 多样个性化标签外挂 留言板 友链 smooth丝滑动画 标签分类与归档 模块窗口划分 评论系统 未来新增功能 开发历程 2025-03-15 ...