补充知识
众所周知(): R θ = [ c o s θ , − s i n θ s i n θ , c o s θ ] R_{\theta} = \begin{bmatrix} cos\theta , -sin\theta \\ sin\theta , cos\theta \end{bmatrix} R θ = [ c o s θ , − s i n θ s i n θ , c o s θ ] 反着转 呢?顺时针旋转 θ \theta θ 嗯?回答我!! R − θ = [ c o s θ , s i n θ − s i n θ , c o s θ ] R_{-\theta} = \begin{bmatrix} cos\theta , sin\theta \\ -sin\theta , cos\theta \end{bmatrix} R − θ = [ c o s θ , s i n θ − s i n θ , c o s θ ] 嗯?你回答我 ,是不是可以把 − θ -\theta − θ R − θ = [ c o s θ , s i n θ − s i n θ , c o s θ ] = R θ T R_{-\theta} = \begin{bmatrix} cos\theta , sin\theta \\ -sin\theta , cos\theta \end{bmatrix} = R_{\theta}^T R − θ = [ c o s θ , s i n θ − s i n θ , c o s θ ] = R θ T 正交矩阵 啦!
小小深入一下三维变换
其实都跟二维差不多
缩放变换(Scaling)和平移变换(Translation)
不多说,自己看
旋转变换(Rotation)
简单旋转
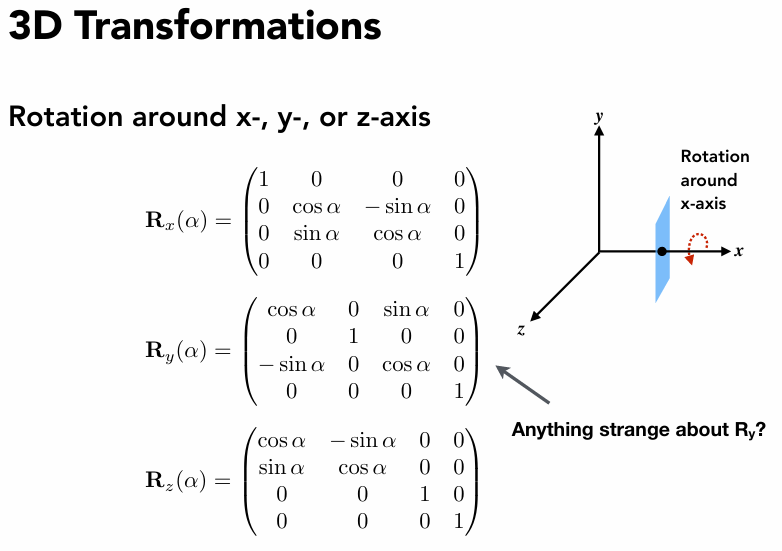
三维的旋转三个轴,先看图
观察发现,绕X轴旋转 R x ( α ) R_x(\alpha) R x ( α ) R y ( α ) R_y(\alpha) R y ( α ) R z ( α ) R_z(\alpha) R z ( α ) R x ( α ) R_x(\alpha) R x ( α ) R y ( α ) R_y(\alpha) R y ( α ) R z ( α ) R_z(\alpha) R z ( α ) α \alpha α x → × y → = z → \overrightarrow{x} \times \overrightarrow{y} = \overrightarrow{z} x × y = z y → × z → = x → \overrightarrow{y} \times \overrightarrow{z} = \overrightarrow{x} y × z = x z → × x → = y → \overrightarrow{z} \times \overrightarrow{x} = \overrightarrow{y} z × x = y 循环对称 的性质(注意:是叉乘哦)
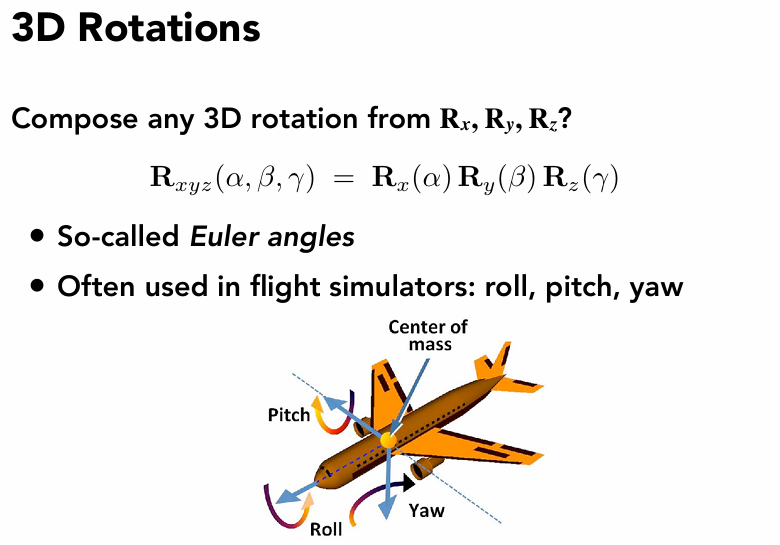
复杂旋转
更多时候,我们不只旋转了一次,不只绕一个轴旋转,那么一样,拆解变换
那么在图形学中,有专门的旋转拆解公式
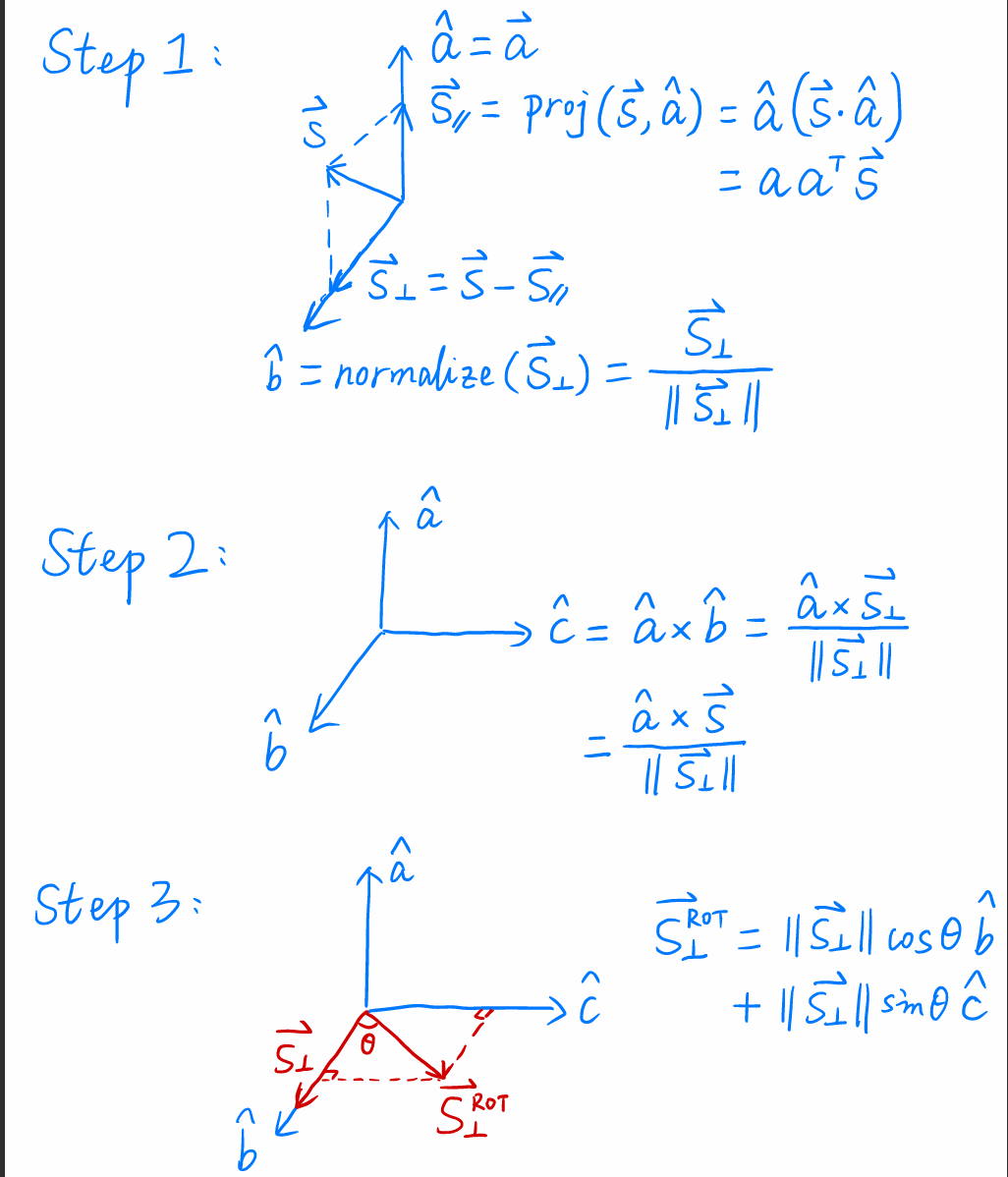
罗德里格斯旋转公式
针对在三维空间中的任意旋转轴的变换,需要用到罗德里格斯旋转公式。
上图部分解释:I 是单位矩阵,n 表示旋转轴向量a → \overrightarrow{a} a s → \overrightarrow{s} s α \alpha α a 与s 不一定垂直),操作如下:
s → \overrightarrow{s} s a 的向量和平行与a 的向量(s → / / \overrightarrow{s}_{//} s / / 向量矩阵化处理:得到的 s → / / = a → ( s → ⋅ a → ) \overrightarrow{s}_{//} = \overrightarrow{a}(\overrightarrow{s}·\overrightarrow{a}) s / / = a ( s ⋅ a ) a a T s → a^T\overrightarrow{s} a T s
垂直分解向量旋转:将分解的垂直向量就可以按照向量的点乘与叉乘在垂直于旋转轴的方向进行旋转。
垂直旋转向量与平行分解向量再次合并,完成旋转
定义相机(Define the camera)
初始定义
位置Position e → \overrightarrow{e} e
镜头朝向Look-at/gaze-direction g → \overrightarrow{g} g
向上方向 Up direction t → \overrightarrow{t} t
相机变换
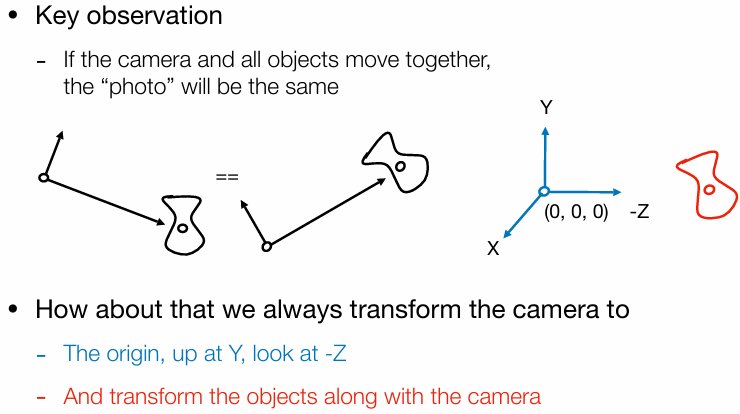
我们都知道相对运动吧,相机动物体不动和物体动相机不动可以展现出相同的画面。
那么我们如何将一个相机放到原点并旋转至我们想要的位置呢? M v i e w = R v i e w T v i e w M_{view} = R_{view}T_{view} M v i e w = R v i e w T v i e w g → \overrightarrow{g} g t → \overrightarrow{t} t
从e点平移回原点,这个很简单
T v i e w = [ 0 , 0 , 0 , − x e 0 , 0 , 0 , − y e 0 , 0 , 0 , − z e 0 , 0 , 0 , 1 ] T_{view} =
\begin{bmatrix}
0 , 0 , 0 , -x_e \\
0 , 0 , 0 , -y_e \\
0 , 0 , 0 , -z_e \\
0 , 0 , 0 , 1
\end{bmatrix}
T v i e w = ⎣ ⎢ ⎢ ⎢ ⎡ 0 , 0 , 0 , − x e 0 , 0 , 0 , − y e 0 , 0 , 0 , − z e 0 , 0 , 0 , 1 ⎦ ⎥ ⎥ ⎥ ⎤
将朝向 g → \overrightarrow{g} g t → \overrightarrow{t} t M v i e w M_{view} M v i e w M v i e w − 1 M_{view}^{-1} M v i e w − 1
M v i e w − 1 = [ x g × t , x t , x − g , 0 y g × t , y t , x − g , 0 z g × t , z t , x − g , 0 0 , 0 , 0 , 1 ] M_{view}^{-1} =
\begin{bmatrix}
x_{g \times t} , x_t , x_{-g} , 0 \\
y_{g \times t} , y_t , x_{-g} , 0 \\
z_{g \times t} , z_t , x_{-g} , 0 \\
0 , 0 , 0 , 1
\end{bmatrix}
M v i e w − 1 = ⎣ ⎢ ⎢ ⎢ ⎡ x g × t , x t , x − g , 0 y g × t , y t , x − g , 0 z g × t , z t , x − g , 0 0 , 0 , 0 , 1 ⎦ ⎥ ⎥ ⎥ ⎤
我们之前也学了,旋转矩阵其实是正交矩阵,那么它的逆矩阵就等于他的转置矩阵,所以我们只需要把上面的逆矩阵转置一下,就直接可以得到我们想要的旋转矩阵!
M v i e w T = R v i e w = [ x g × t , y g × t , z g × t , 0 x t , y t , z t , 0 x − g , y − g , x − g , 0 0 , 0 , 0 , 1 ] M_{view}^T = R_{view} =
\begin{bmatrix}
x_{g \times t} , y_{g \times t} , z_{g \times t} , 0 \\
x_t , y_t , z_t , 0 \\
x_{-g} , y_{-g} , x_{-g} , 0 \\
0 , 0 , 0 , 1
\end{bmatrix}
M v i e w T = R v i e w = ⎣ ⎢ ⎢ ⎢ ⎡ x g × t , y g × t , z g × t , 0 x t , y t , z t , 0 x − g , y − g , x − g , 0 0 , 0 , 0 , 1 ⎦ ⎥ ⎥ ⎥ ⎤
总概
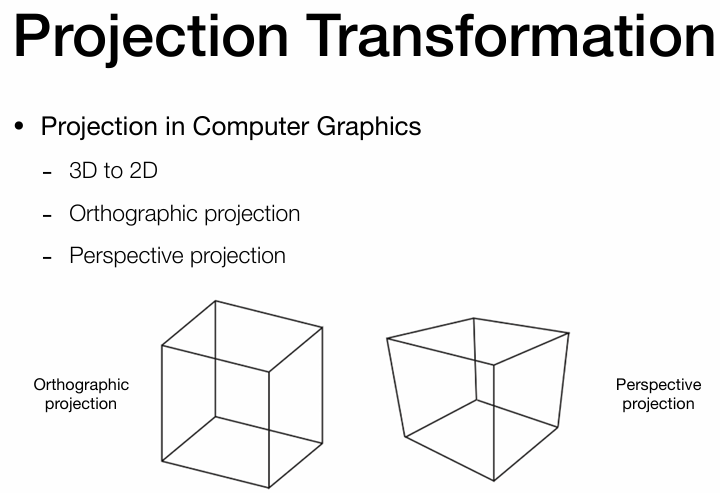
投影方式分为两种:
正交投影(Orthographic projection) 透视投影(Perspective projecttion)
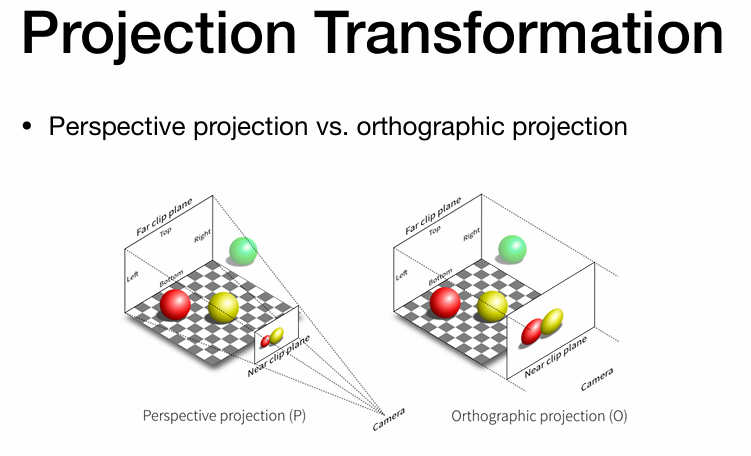
正交与透视二者区别
视觉效果 :
正交并不会带来一种现象:近大远小,更多出现在工程制图。人眼更接近的是右侧的透视投影,会有这个现象。图形学里的数学做法 :
左侧的透视投影,我们认为相机在空间的某一点,由此在空间方向上延伸出一个四棱锥,把从一个深度区域到另一个深度的这一块区域里的东西显示出来,在四棱锥近处的一个平面屏幕上得到所照的图像。
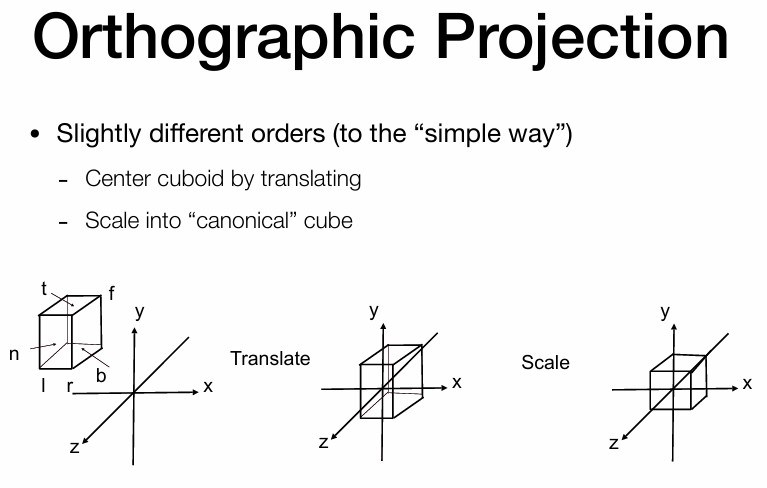
正交投影(Orthographic projection)
A simple way*
首先,正常相机放在原点,朝向-z方向,向上方向为y方向。
丢去z轴,这样所有东西都直接得到在成像平面上的样子
在移动到 [ − 1 , 1 ] 2 [-1,1]^2 [ − 1 , 1 ] 2
图形学正式的做法
定义立方体:[ l , r ] x [ b , t ] x [ f , n ]
移动立方体
缩放变成正则立方体 [ − 1 , 1 ] 3 [-1,1]^3 [ − 1 , 1 ] 3 f , n ],far远处坐标比近处near要小,这是定义过程。f 和n 就是反着的。
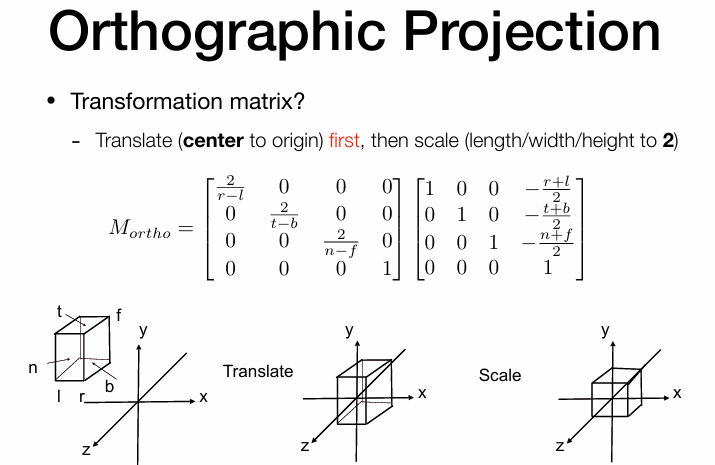
具体的矩阵运算操作 :
T o r t h o = [ 1 , 0 , 0 , − r + l 2 0 , 1 , 0 , − t + b 2 0 , 0 , 1 , − n + f 2 0 , 0 , 0 , 1 ] T_{ortho} =
\begin{bmatrix}
1 , 0 , 0 , -\frac{r + l}{2} \\
0 , 1 , 0 , -\frac{t + b}{2} \\
0 , 0 , 1 , -\frac{n + f}{2} \\
0 , 0 , 0 , 1
\end{bmatrix}
T o r t h o = ⎣ ⎢ ⎢ ⎢ ⎡ 1 , 0 , 0 , − 2 r + l 0 , 1 , 0 , − 2 t + b 0 , 0 , 1 , − 2 n + f 0 , 0 , 0 , 1 ⎦ ⎥ ⎥ ⎥ ⎤
后缩放
S o r t h o = [ 2 r − l , 0 , 0 , 0 0 , 2 t − b , 0 , 0 0 , 0 , 2 n − f , 0 0 , 0 , 0 , 1 ] S_{ortho} =
\begin{bmatrix}
\frac{2}{r-l} , 0 , 0 , 0 \\
0 , \frac{2}{t-b} , 0 , 0 \\
0 , 0 , \frac{2}{n-f} , 0 \\
0 , 0 , 0 , 1
\end{bmatrix}
S o r t h o = ⎣ ⎢ ⎢ ⎢ ⎡ r − l 2 , 0 , 0 , 0 0 , t − b 2 , 0 , 0 0 , 0 , n − f 2 , 0 0 , 0 , 0 , 1 ⎦ ⎥ ⎥ ⎥ ⎤
最终结果:
M o r t h o = S o r t h o T o r t h o = [ 2 r − l , 0 , 0 , 0 0 , 2 t − b , 0 , 0 0 , 0 , 2 n − f , 0 0 , 0 , 0 , 1 ] [ 1 , 0 , 0 , − r + l 2 0 , 1 , 0 , − t + b 2 0 , 0 , 1 , − n + f 2 0 , 0 , 0 , 1 ] M_{ortho} =
S_{ortho} T_{ortho} =
\begin{bmatrix}
\frac{2}{r-l} , 0 , 0 , 0 \\
0 , \frac{2}{t-b} , 0 , 0 \\
0 , 0 , \frac{2}{n-f} , 0 \\
0 , 0 , 0 , 1
\end{bmatrix}
\begin{bmatrix}
1 , 0 , 0 , -\frac{r + l}{2} \\
0 , 1 , 0 , -\frac{t + b}{2} \\
0 , 0 , 1 , -\frac{n + f}{2} \\
0 , 0 , 0 , 1
\end{bmatrix}
M o r t h o = S o r t h o T o r t h o = ⎣ ⎢ ⎢ ⎢ ⎡ r − l 2 , 0 , 0 , 0 0 , t − b 2 , 0 , 0 0 , 0 , n − f 2 , 0 0 , 0 , 0 , 1 ⎦ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ 1 , 0 , 0 , − 2 r + l 0 , 1 , 0 , − 2 t + b 0 , 0 , 1 , − 2 n + f 0 , 0 , 0 , 1 ⎦ ⎥ ⎥ ⎥ ⎤
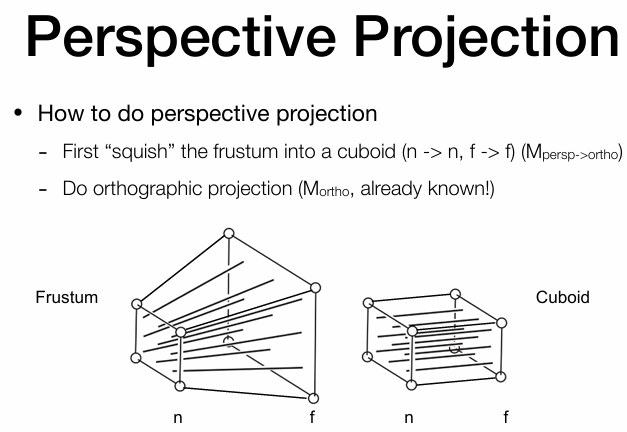
透视投影(Perspective projecttion)
小知识回顾
在三维中,可以定义一个点是(x,y,z,1),(kx,ky,kz,k!=0),那么是不是也可表示为(zx,zy,z 2 z^2 z 2
原理讲述
看上面的图,
将透视投影转变到正交投影,也就是 M p e r s p − > o r t h o M_{persp->ortho} M p e r s p − > o r t h o
再正常做一次正交投影 M o r t h o M_{ortho} M o r t h o
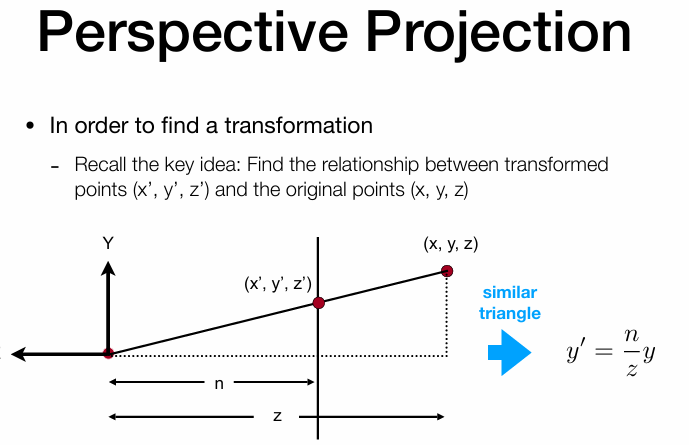
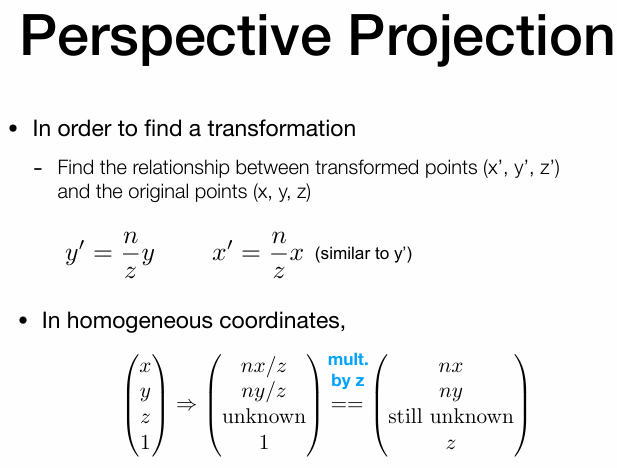
从侧面开始看,那么我们所需观测的就是(x’,y’,z’)到(x,y,z)这一区间,问题是将(x,y,z)挤压。y ′ = n z y y' = \frac{n}{z}y y ′ = z n y x ′ = n z x x' = \frac{n}{z}x x ′ = z n x
其实通过以上推导就可以得出 M p e r s p − > o r t h o M_{persp->ortho} M p e r s p − > o r t h o
现在的问题是得出第三行的内容。这个时候我们需要观察
near面上的点没用动
far面上的点的z没有动
( n x n y u n k n o w z ) − − > ( x y n 1 ) = ( n x n y n 2 n ) \begin{pmatrix}
nx \\
ny \\
unknow \\
z
\end{pmatrix} -->
\begin{pmatrix}
x \\
y \\
n \\
1
\end{pmatrix} =
\begin{pmatrix}
nx \\
ny \\
n^2 \\
n
\end{pmatrix}
⎝ ⎜ ⎜ ⎜ ⎛ n x n y u n k n o w z ⎠ ⎟ ⎟ ⎟ ⎞ − − > ⎝ ⎜ ⎜ ⎜ ⎛ x y n 1 ⎠ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎜ ⎛ n x n y n 2 n ⎠ ⎟ ⎟ ⎟ ⎞
那么其实可以知道矩阵第三行其实就是(0,0,A,B)的一种形式
( 00 A B ) ( x y n 1 ) = n 2 (0 0 A B)
\begin{pmatrix}
x \\
y \\
n \\
1
\end{pmatrix} =
n^2
( 0 0 A B ) ⎝ ⎜ ⎜ ⎜ ⎛ x y n 1 ⎠ ⎟ ⎟ ⎟ ⎞ = n 2
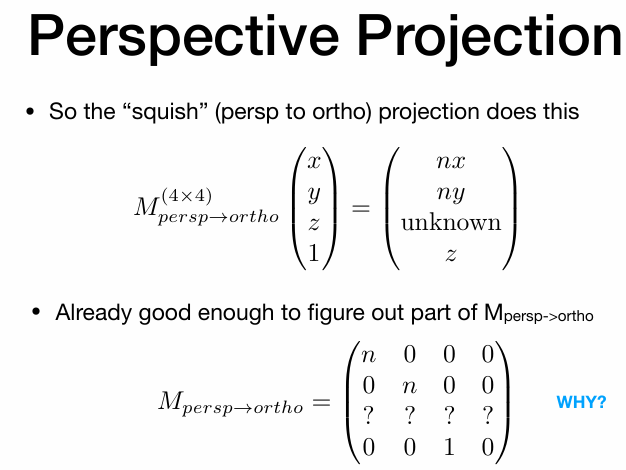
再根据上面注意到的内容,就可以得出:n 2 n^2 n 2 f 2 f^2 f 2 M p e r s p − > o r t h o M_{persp->ortho} M p e r s p − > o r t h o
M p e r s p − > o r t h o = [ n , 0 , 0 , 0 0 , n , 0 , 0 0 , 0 , n + f , − n f 0 , 0 , 1 , 0 ] M_{persp->ortho} =
\begin{bmatrix}
n , 0 , 0 , 0 \\
0 , n , 0 , 0 \\
0 , 0 , n+f , -nf \\
0 , 0 , 1 , 0
\end{bmatrix}
M p e r s p − > o r t h o = ⎣ ⎢ ⎢ ⎢ ⎡ n , 0 , 0 , 0 0 , n , 0 , 0 0 , 0 , n + f , − n f 0 , 0 , 1 , 0 ⎦ ⎥ ⎥ ⎥ ⎤
然后最终的投影变换 M p e r s p = M o r t h o M p e r s p − > o r t h o M_{persp} = M_{ortho} M_{persp->ortho} M p e r s p = M o r t h o M p e r s p − > o r t h o
M p e r s p = M o r t h o M p e r s p − > o r t h o = [ 2 r − l , 0 , 0 , − r + l 2 0 , 2 t − b , 0 , − t + b 2 0 , 0 , 2 n − f , − n + f 2 0 , 0 , 0 , 1 ] [ n , 0 , 0 , 0 0 , n , 0 , 0 0 , 0 , n + f , − n f 0 , 0 , 1 , 0 ] M_{persp} =
M_{ortho} M_{persp->ortho} =
\begin{bmatrix}
\frac{2}{r-l} , 0 , 0 , -\frac{r + l}{2} \\
0 , \frac{2}{t-b} , 0 , -\frac{t + b}{2} \\
0 , 0 , \frac{2}{n-f} , -\frac{n + f}{2} \\
0 , 0 , 0 , 1
\end{bmatrix}
\begin{bmatrix}
n , 0 , 0 , 0 \\
0 , n , 0 , 0 \\
0 , 0 , n+f , -nf \\
0 , 0 , 1 , 0
\end{bmatrix}
M p e r s p = M o r t h o M p e r s p − > o r t h o = ⎣ ⎢ ⎢ ⎢ ⎡ r − l 2 , 0 , 0 , − 2 r + l 0 , t − b 2 , 0 , − 2 t + b 0 , 0 , n − f 2 , − 2 n + f 0 , 0 , 0 , 1 ⎦ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ n , 0 , 0 , 0 0 , n , 0 , 0 0 , 0 , n + f , − n f 0 , 0 , 1 , 0 ⎦ ⎥ ⎥ ⎥ ⎤
结束!
变换到此暂时结束的寄语
整体难度还行,认真推导的话会发现很简单,这也只是皮毛,后面还会深入
ArisuMika
关注Arisu喵!关注Arisu谢谢喵!