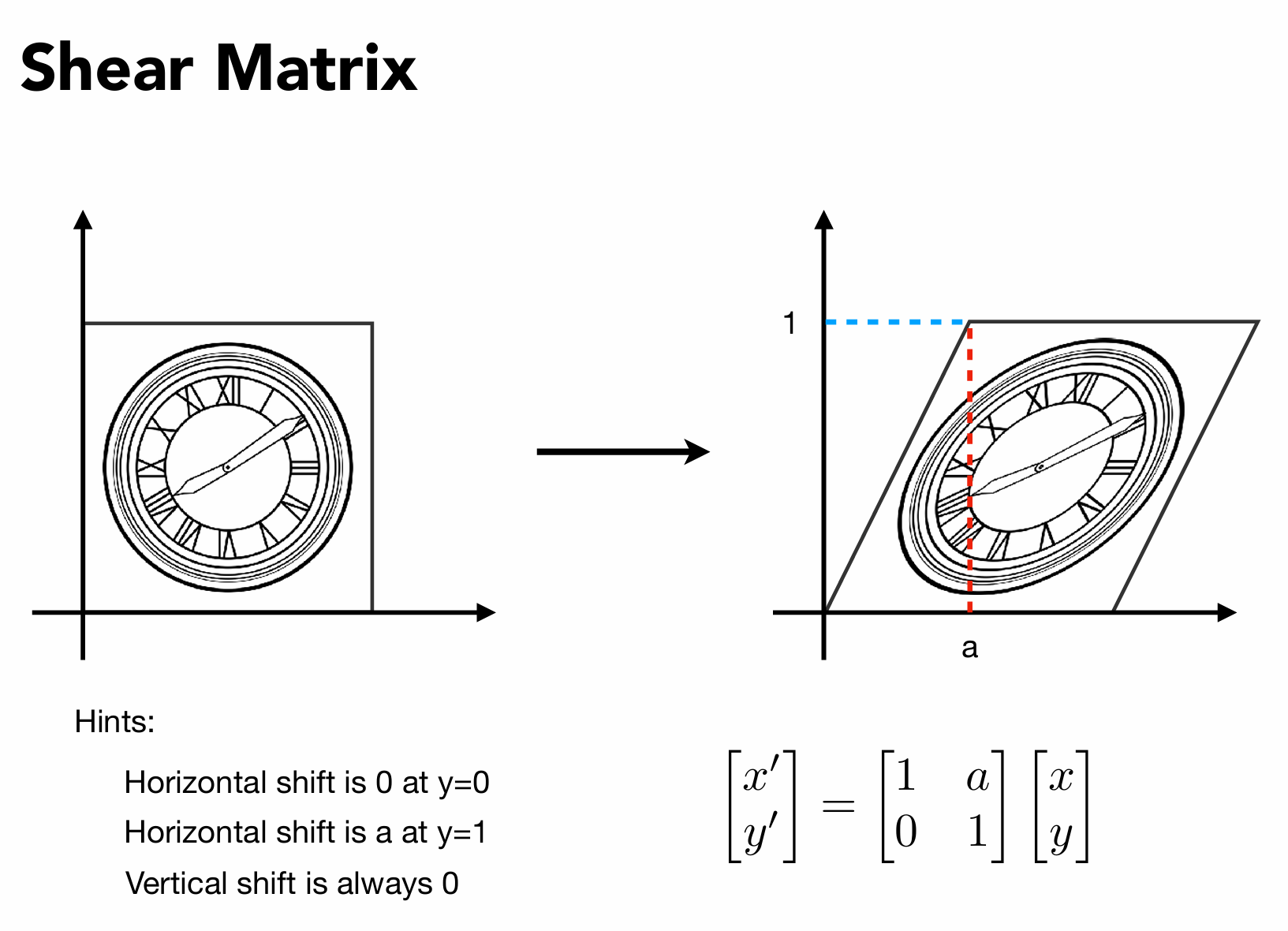
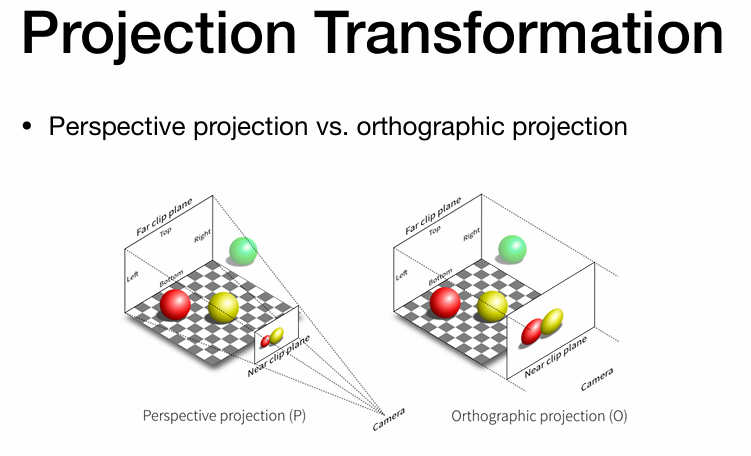
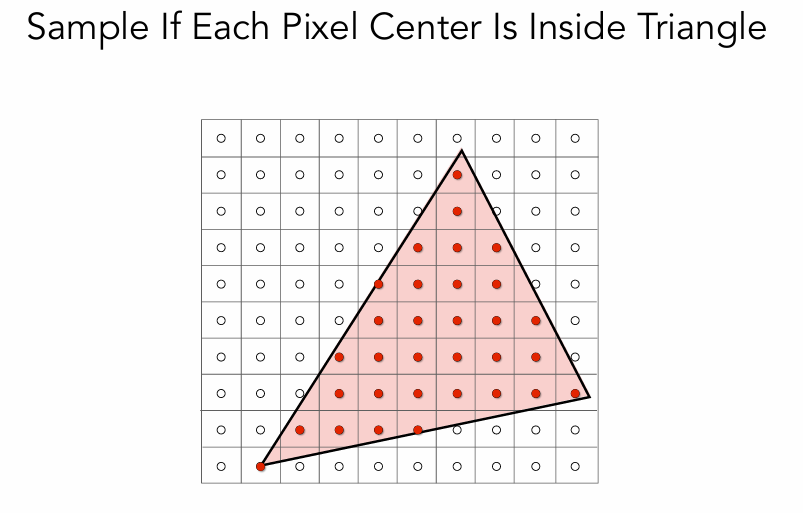
光栅化(三角形的离散化)
在之前的视图变换之后就要进行光栅化
视锥
视锥定义
从摄像机出发,看到的第一个平面是近平面,那么我们要给近平面定义一个宽高度,就类似于显示器一样的宽高比。
也就是可以看到的角度范围:fov,一般分为fovY和fovX。
foxY就是垂直可视角度;fovX也就是水平可视角度。
一般定义宽高比和fovY,直接就可以推出fovX。
具体可以看下图:
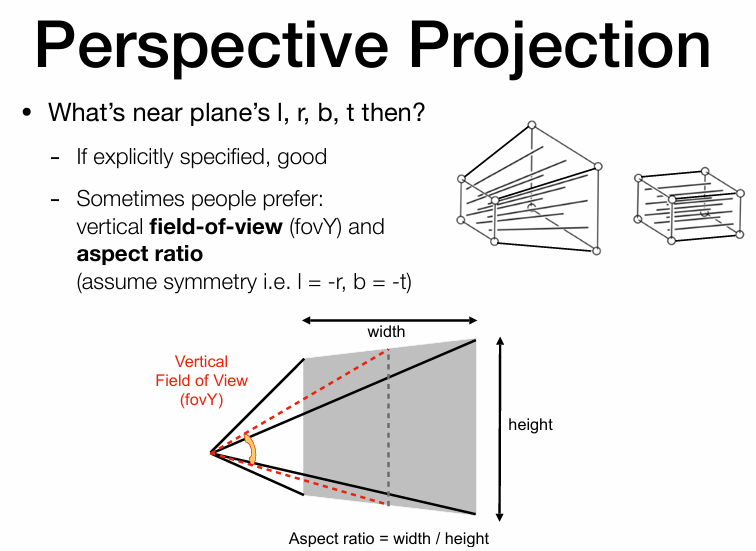
视锥计算
确定fovY之后,就可以知道上面角度就是fovY/2,假定近平面上中点坐标是(0,t,n).
就可以列出等式:
宽高比:aspect =
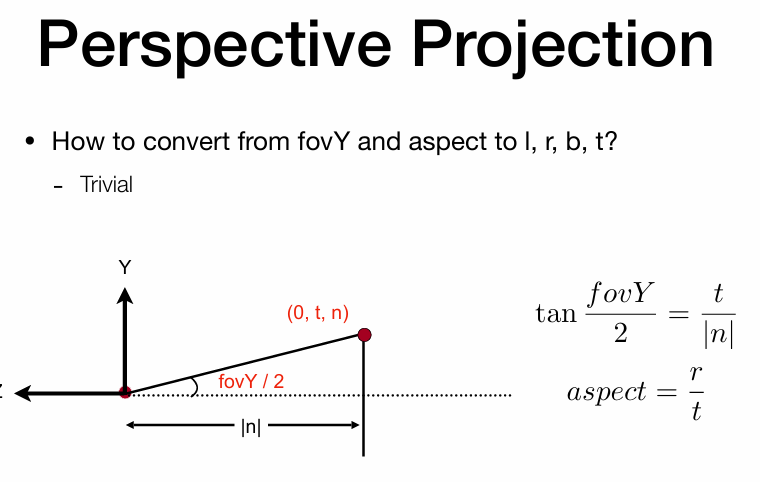
这些概念都可以相互转换
光栅化(三角形的离散化)
做完MVP(模型、视图、投影变换)
参考本篇文章:变换(模型、视图、投影)
做完上述变换之后,所有的物体都会停留在 的立方体里面。
那么这个一个正方体应该画在哪里呢?那肯定是在屏幕上。
显示在屏幕上
基本概念
什么是屏幕?
- 屏幕由一组像素组成
- 分辨率:像素组的数量密度
- 屏幕是典型的光栅成像设备
Raster"光栅化"
- Ratherize == 画到屏幕上
像素
一个像素显示一种颜色;像素颜色由RGB(red,green,blue)混合组成。
定义屏幕空间
定义一个平面直角坐标系,每个像素都可以用坐标来表示,写成(x,y)形式。
例如下图的蓝色像素可以用(2,1)来表示
从零开始,像素的坐标范围就是(0,0)到(width-1,height-1)
像素的的中心就是(x+0.5,y+0.5)
屏幕的覆盖范围则是(0,0)到(width,height)

映射到屏幕空间
相机朝向在z上,我们先不管
那么就很简单了,在x,y上变换:
将xy: 变换到 [0,width] * [0,height]
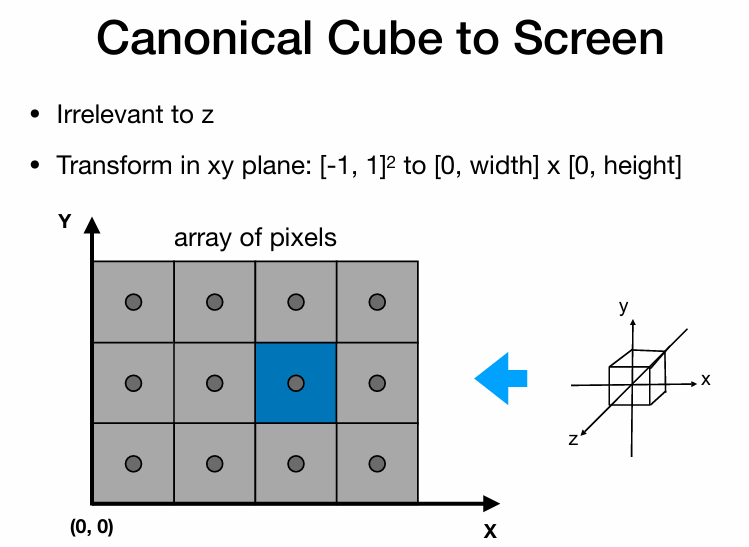
那么就可以得到视口变换:
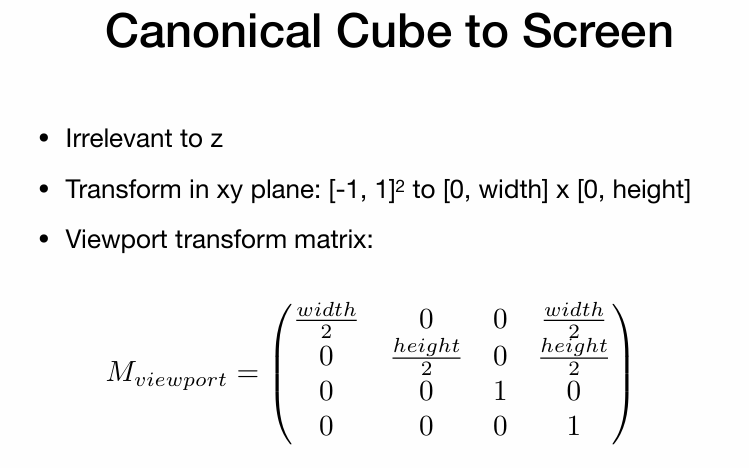
基础图形(三角形)
在计算机图形中,最基本的图形就是三角形,得到非常广泛的运用。
- 三角形是最基础的多边形。
- 任何的多边形都可以拆解成三角形。
- 三个点连成三角形,那一定是一个平面。
- 三角形的内部是一个平面。
- 三角形的内外部定义非常清楚,通过向量叉积就可以了。
- 只要定义三个顶点,就可以推算出三角形内的任何一个点。
最简单的光栅化(采样)
采样:就是把一个函数离散化的过程。
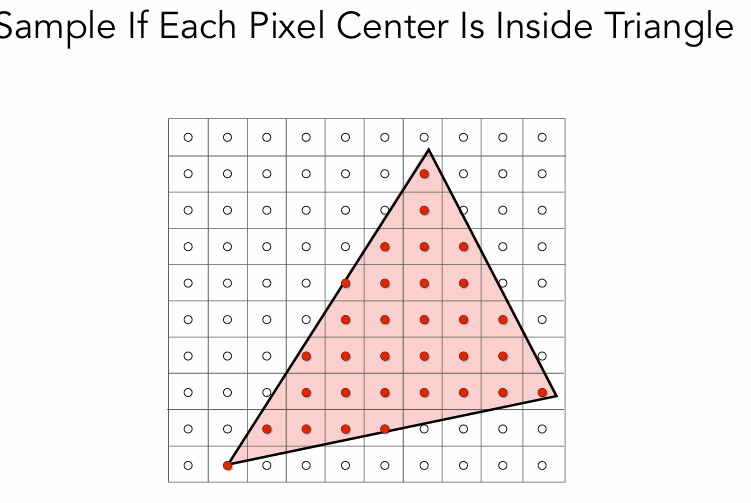
光栅化采样:利用像素的中心,对屏幕空间进行采样。
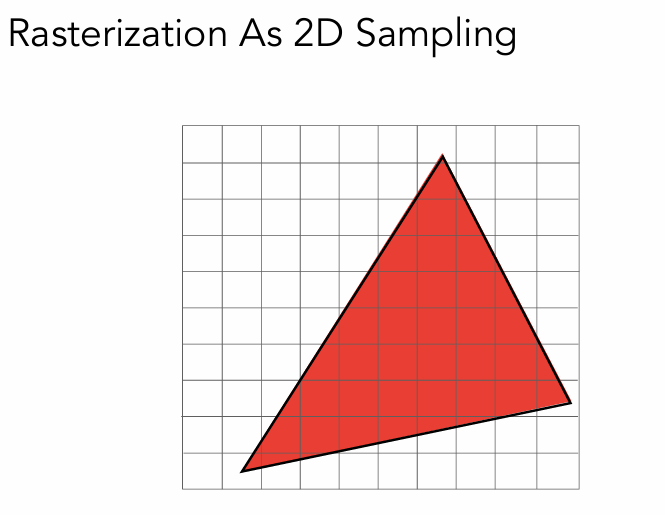
假如我们需要对上面的三角形进行采样,光栅化显示在屏幕上。
定义一个函数:inside(tri,x,y),判断像素点是否在三角形内,
在三角形内就是1,不在就是0.
跟据1和0的判断,就可以进行采样离散化。
采样函数belike:
1 | for (int x = 0; x < xmax; x++) |
那么inside的函数具体是怎么实现的呢?
其实之前学向量的叉积的时候就提到过了。

具体计算过程参考这篇文章:线性代数:向量与基础矩阵
光栅采样中的争议问题
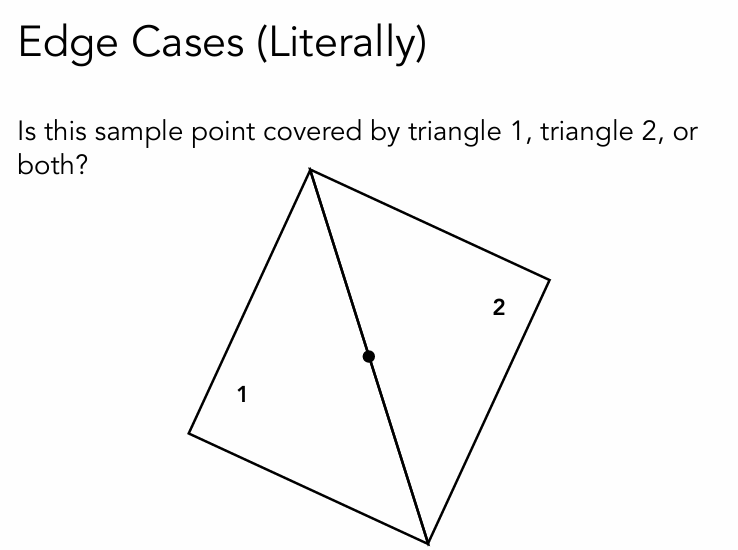
像下面的这幅图,中间的点到底是在三角形1 还是 2 还是 都在 还是 都不在。
这些! 全部自己决定!
- 注意:在一些图形学的API上,比如OpenGl或者Direct X,有非常严格的规定,点在上左则算在内,下右不算。
最简单的加速优化?
一优化:
我们得到采样之后的数据之后,是否有必要遍历全部像素点?
只需要如下图的选择xmax和ymax的矩形(蓝色区域)中遍历就可以了。也就是使用包围盒,Bounding Box。

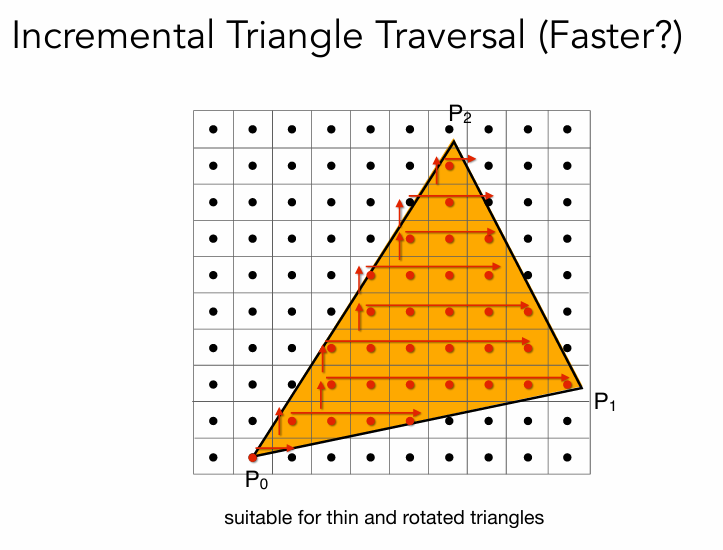
二优化:
去选择每一行的xmin和xmax,然后直接在这区间内给像素着色就可以了。
每一行都记录这xmin和xmax,保证遍历的像素点最少。
但是并不好实现,一般在bounding box非常大的情况下使用。
锯齿
经过以上步骤,恭喜你!完成了光栅化的基础采样,并显示在了屏幕之上,但是结果是下图的样子。
我们想要的明明是一个平整的三角形,这是为什么呢?
锯齿产生了!光栅化图形学一直在致力于解决的严重问题。
锯齿产生的原因,像素本身自己有一定的大小,采样率对于信号也不够高,产生了走样的结果。

之后
接下来要解决 抗锯齿 或者是 反走样!!!
ArisuMika
关注Arisu喵!关注Arisu谢谢喵!