线性代数:向量与基础矩阵
向量
向量加法
不多说,直接加就是了
平行四边形法则或者三角形法则
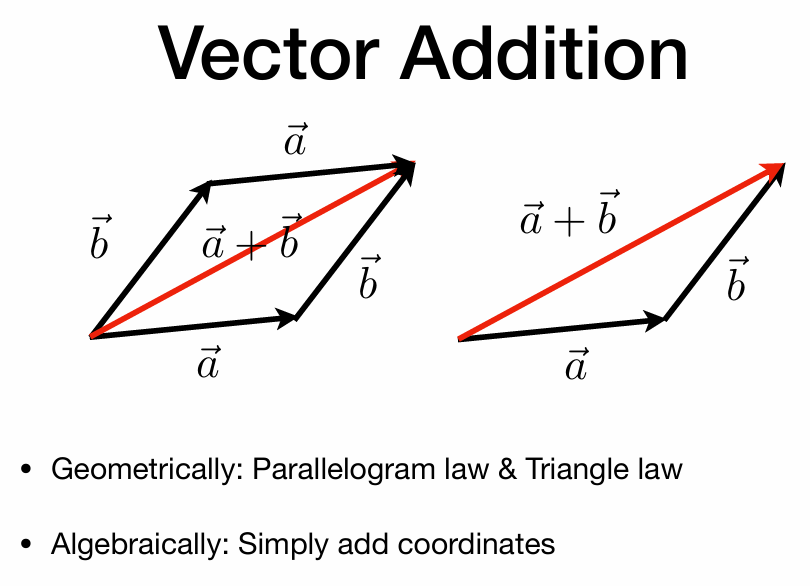
向量点乘
也没什么好说的,高中数学
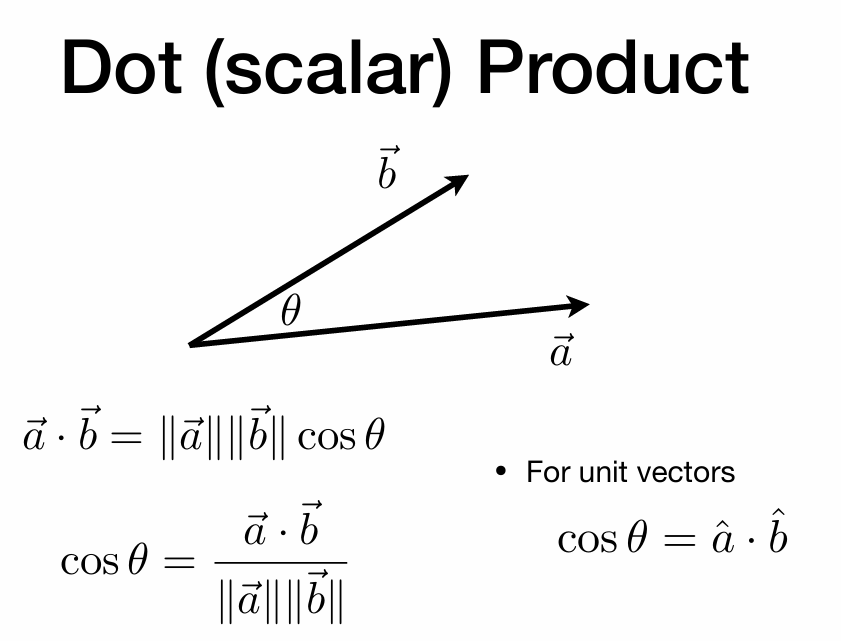

有什么用
可以通过向量点乘来判断向量间的夹角,两向量的方向关系
向量叉乘*
叉乘和点乘是完全不一样的计算,向量叉乘仅在三维空间中有定义。对于两个向量a = ()和b=(),它们的叉乘 的结果垂直于 和 。
1.几何意义
垂直性:叉乘的结果向量垂直于原向量,并且其方向由右手(螺旋)法则(四指从前乘绕向后乘,大拇指方向即为所得叉乘向量方向)决定。
模长:叉乘的模长等于两个向量所构成的平行四边形的面积,即:
其中 是两向量之间的夹角。
2.运算性质
反交换律:
分配律:
与标量乘法结合:

3.利用叉乘可以构建三维坐标系

4.在图形学应用:判断向量方位/判断点与面与向量位置
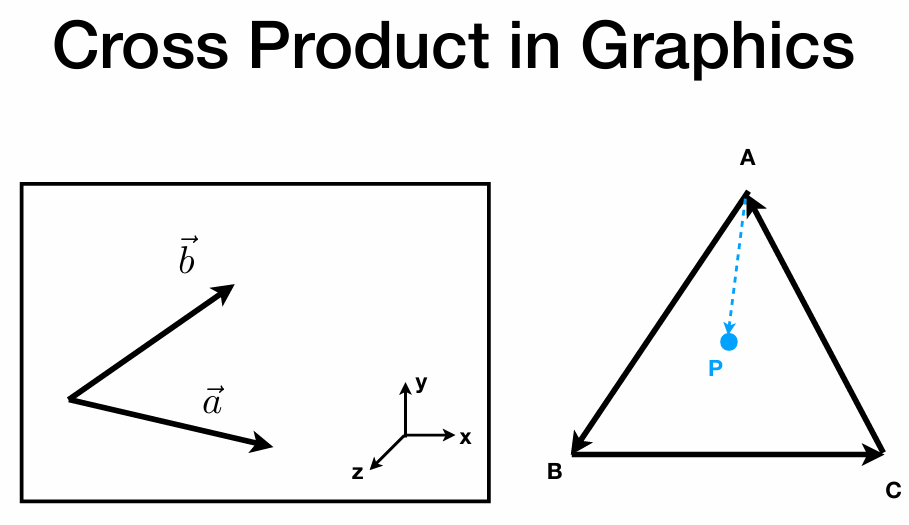
问题参考下图:
- 向量方位(看左图):
如果 所得的c是正的,那么可以判断b在a的左侧
如果反过来, 所得的c是负的,那么可以判断a在b的右侧
(可以自己用右手法则验证一下) - 点与面的位置(看右图):
和 和 所得的结果都是同侧,那么可以判断P点在 中
如果其中任何一个值表示另一侧,则P不在 中
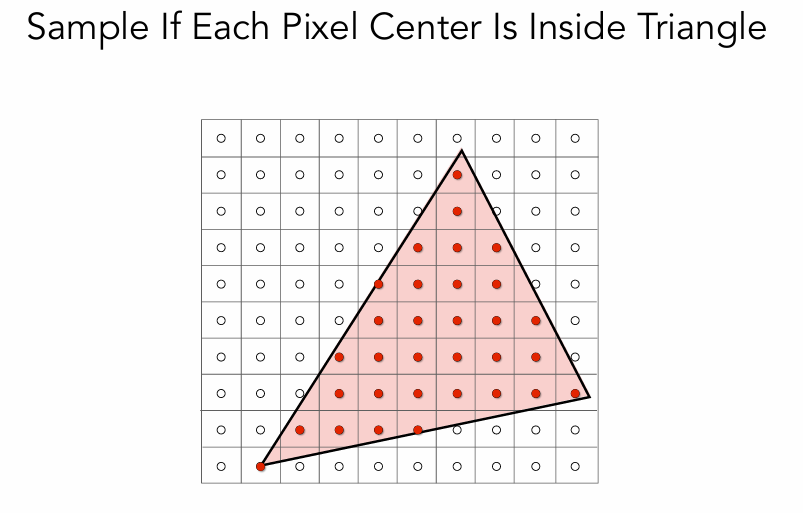
以上知识在图形学中的重点
例如做三角形的光栅化,要判断三角形覆盖了哪些像素点,要知道像素是否在三角形内部,对像素进行着色
矩阵(基础部分)
不多说,大一线代知识
矩阵相乘
计算方法
如下图:
要算C第几行第几列就去找前面A第几行和B第几列

性质:
如下图:

矩阵与向量
其实跟矩阵相乘差不多,只不过有一个矩阵变成了1*n的向量,不多说
转置矩阵

单位矩阵与矩阵的逆
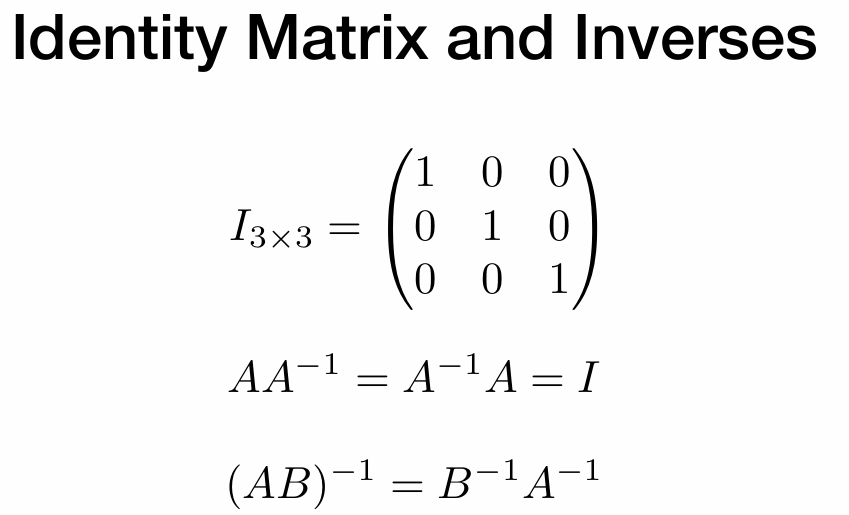
向量相乘表示为矩阵相乘

ArisuMika
关注Arisu喵!关注Arisu谢谢喵!
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 ArisuMika'Blog!
评论